机器学习、深度学习领域中，梯度下降（Gradient descent）算法被广泛应用，它是一种用于优化问题的算法，目的是找到一个函数的最小值。它是一种优化算法，通常用于训练机器学习模型和神经网络。它通过最大限度地减少预测结果和实际结果之间的误差来训练机器学习模型。本篇我们一起来看看应该如何运用梯度下降算法解决问题。

01 什么是梯度下降算法

梯度下降算法是一种迭代优化算法，用于找到一个可微分函数的最小值。它的基本思想是：从一个初始点开始，沿着函数梯度的反方向（下坡）逐步移动，直到找到函数的局部最小值。

1. 我们举一个例子说明：

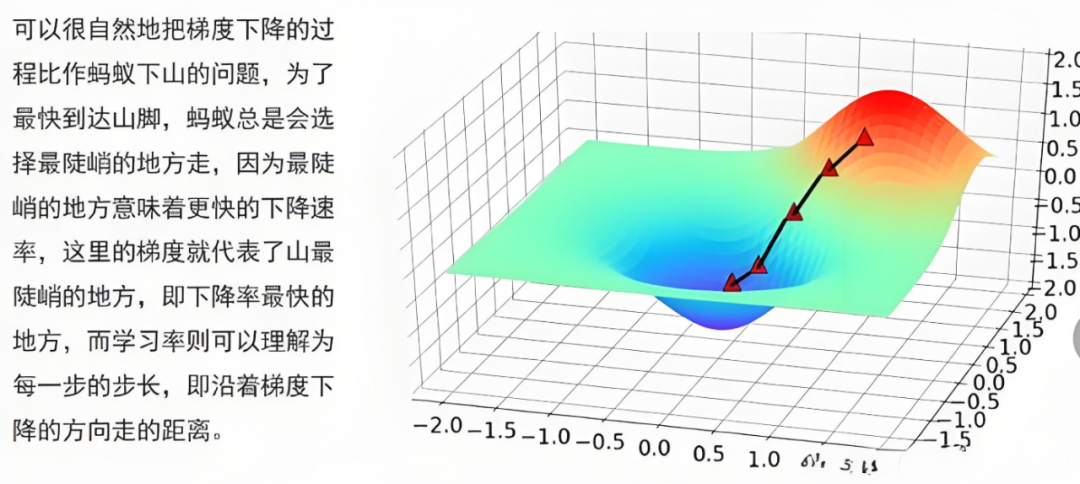
假如你在一座高山上，目标是下山，找到山脚的最低点。你站在山顶，周围一片雾气，看不清远处的路，只能看到脚下的坡度。你希望尽快下山，找到最低点。我们在这里引申两个概念。

  • 梯度：就是你脚下坡度的方向和陡峭程度。如果坡很陡，说明梯度大；如果坡很缓，说明梯度小。梯度的方向（指向山顶）总是指向函数值增加最快的方向，而梯度的反方向（指向山脚）则是函数值减少最快的方向。
  • 下降：因为你目标是找到最低点，所以你需要沿着梯度的反方向（下山方向）走。
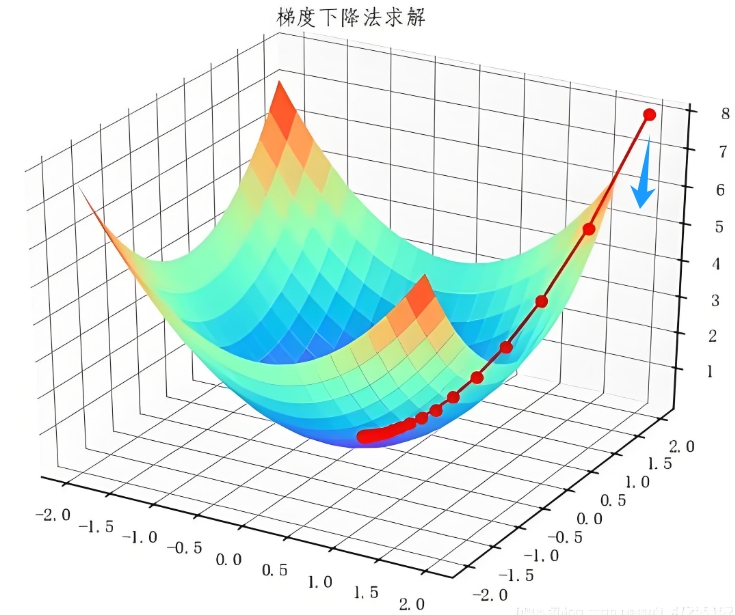
机器学习AI开发之【梯度下降】算法，可以这样读懂它

2. 我们再来看看梯度下降的过程：

（1） 初始位置：假如你站在山顶，这就是算法的初始点。

（2） 观察坡度：你看看脚下，判断坡度的方向和陡峭程度，这就是计算梯度的过程。

（3） 迈出一步：你沿着坡度的反方向（即下坡方向）迈出一步。这一步的大小很重要，如果迈得太大，可能会直接越过最低点；如果迈得太小，下山速度又太慢。这个步长在算法中被称为“学习率”。

（4）重复过程：每走一步，你都重新观察坡度，再沿着新的下坡方向迈出一步，直到你感觉脚下已经没有明显的下坡方向了，或者你已经走得足够远了，认为已经到达最低点。

机器学习AI开发之【梯度下降】算法，可以这样读懂它

3. 在数学上，我们可以这样理解：

假设有一个函数 f(x)，你想找到它的最小值。梯度下降算法的步骤如下：

（1） 选择初始点：随便选一个点 x0。

（2） 计算梯度：在 x0 处计算函数的导数（梯度），记为 ∇f(x0)。

（3） 更新位置：根据梯度的反方向更新位置，公式是 x1=x0−α∇f(x0)，其中 α 是学习率。

（4） 重复步骤：在新的位置 x1 处重复计算梯度，更新位置，直到梯度接近零，或者满足其他停止条件。

机器学习AI开发之【梯度下降】算法，可以这样读懂它

02 应用场景

梯度下降算法是一种非常通用的优化算法，广泛应用于需要找到函数最小值的场景。以下是一些常见的应用场景：

1. 机器学习中的参数优化

在机器学习中，我们通常需要训练模型以最小化损失函数（Loss Function），梯度下降算法是实现这一目标的核心工具。

(1) 线性回归：其目标是找到最佳的回归线，使预测值与真实值之间的误差最小。

(2) 逻辑回归：目标是训练一个分类模型，将数据划分为不同的类别。

(3) 神经网络训练：目标是训练神经网络，使其能够准确地对输入数据进行分类或回归。

2. 深度学习中的优化

在深度学习中，梯度下降算法及其变体（如随机梯度下降、Adam优化器等）是训练深度神经网络的核心方法。

(1) 卷积神经网络（CNN）：目标是训练用于图像识别、分类等任务的模型。

(2) 循环神经网络（RNN）：目标是训练用于处理序列数据（如文本、语音）的模型。

3. 图像处理

在图像处理中，梯度下降算法可以用于优化图像分割、图像重建等问题。

(1) 图像分割：目标是将图像分割成不同的区域。

(2) 图像重建：目标是从损坏或模糊的图像中重建出清晰的图像。

4. 物理模拟

在物理模拟中，梯度下降算法可以用于优化系统的能量分布、路径规划等问题，例如为机器人或自动驾驶车辆规划最优路径。

5. 小结

梯度下降算法是一种非常通用的优化工具，适用于任何需要最小化目标函数的场景。它在机器学习、深度学习、图像处理、信号处理、金融、工程、物理模拟和经济学等领域都有广泛的应用。

机器学习AI开发之【梯度下降】算法，可以这样读懂它

03 算法实现

下面是一个使用 PyTorch 实现梯度下降算法的简单示例。我们将通过一个简单的线性回归问题来演示如何使用梯度下降算法找到最优参数。

1. 问题描述

假设我们有一个线性模型 y=w⋅x+b，其中 w 是权重，b 是偏置。我们的目标是通过梯度下降算法找到最优的 w 和 b，使得模型的预测值与真实值之间的误差最小。

2. 数据准备

我们将生成一些简单的线性数据，并添加一些噪声。

3. 梯度下降的实现

我们将手动实现梯度下降算法，而不是使用 PyTorch 的优化器。

以下是完整的代码：

import torch
# 设置随机种子以保证结果可复现torch.manual_seed(42)
# 生成数据# 真实的线性关系为 y = 2x + 1true_w = 2.0true_b = 1.0x = torch.randn(100, 1)  # 生成100个随机数据点y = true_w * x + true_b + 0.1 * torch.randn(100, 1)  # 添加噪声
# 初始化参数w = torch.randn(1, requires_grad=True)  # 权重b = torch.randn(1, requires_grad=True)  # 偏置
# 学习率learning_rate = 0.1
# 训练过程num_epochs = 100  # 迭代次数for epoch in range(num_epochs):    # 前向传播：计算预测值    y_pred = w * x + b    # 计算损失函数（均方误差）    loss = torch.mean((y_pred - y) ** 2)
    # 反向传播：计算梯度    loss.backward()
    # 手动更新参数    with torch.no_grad():  # 禁用梯度计算        w -= learning_rate * w.grad        b -= learning_rate * b.grad        # 清空梯度        w.grad.zero_()        b.grad.zero_()
    # 打印损失    if (epoch + 1) % 10 == 0:        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}, w: {w.item():.4f}, b: {b.item():.4f}')
# 打印最终结果print(f'Final w: {w.item():.4f}, Final b: {b.item():.4f}')

4. 代码解释

（1）数据生成：

我们生成了 100 个随机数据点 x，并根据线性关系 y=2x+1 生成了对应的 y，同时添加了一些噪声。

（2）参数初始化：

权重 w 和偏置 b 被随机初始化，并设置 `requires_grad=True`，这样 PyTorch 会自动计算它们的梯度。

（3）学习率：学习率决定了每次更新参数的步长。

（4）训练过程：在每次迭代中，进行以下步骤。

  • 计算预测值 ypred。
  • 计算损失函数（均方误差）。
  • 调用 `loss.backward()` 计算梯度。
  •  手动更新参数 w 和 b，并清空梯度。

（5）打印结果：

  • 每隔 10 次迭代打印一次损失、当前权重和偏置。
  • 最终打印出训练后的权重和偏置。

5. 输出结果

运行上述代码后，你将看到损失逐渐减小，最终 w 和 b 接近真实值 2.0 和 1.0。

6. 注意事项

  • 学习率：学习率的选择非常重要。如果学习率太大，可能导致参数更新过快，无法收敛；如果学习率太小，收敛速度会很慢。
  • 手动清空梯度：在每次更新参数后，需要手动清空梯度，否则梯度会累积。

来源：码农随心笔记